資料分析流程、探索式資料分析(EDA)

• 資料分析基本流程
• 探索式資料分析(EDA)
  敘述統計 Descriptive statistics
  資料視覺化 Data visualization

進行機器學習的模型建立前，了解一下我們手中的資料是必要的過程，所以今天來講一下「探索式資料分析(EDA)」。

資料分析基本流程

在開始機器學習前，我們先來看看資料分析的基本流程: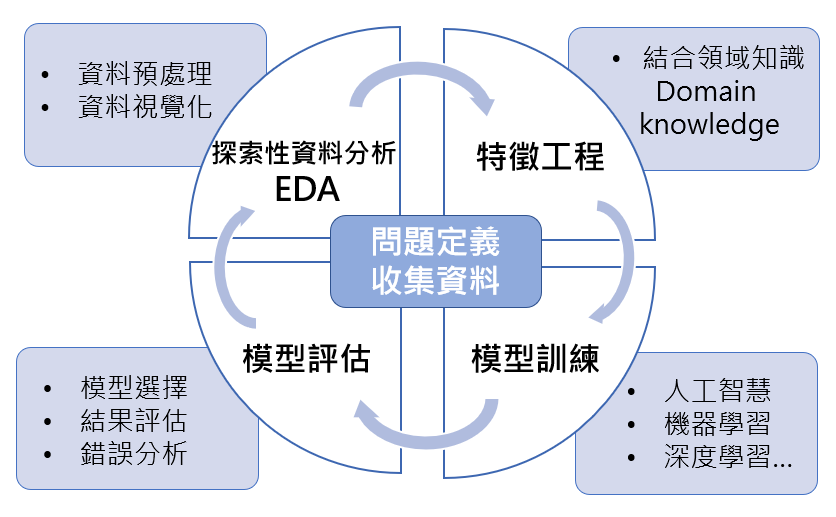

在進行資料分析前，首先需要做的就是確認問題，訂定好我們的目標(Target, Y)，然後才去收集資料，拿到資料後才開始我們的資料分析流程。

1. 探索式資料分析 (Exploratory Data Analysis, EDA)
   收集到的原始資料往往不太乾淨，或資料的形式並不是我們想要的模樣，所以就要去做資料的前處理(資料擷取、清理、整合、遺失直填補...)。進行探索式資料分析可以幫助了解資料處理的狀況，還有整體的趨勢等等。
2. 特徵工程 (Feature Engineering)
   拿到的資料可能會有許多的變數，這時候選出切合問題的特徵變數就很重要了，我們可以向領域相關的專家諮詢，結合他們的意見和經驗去進行選擇。
3. 模型訓練 (Model Traning)
   接下來就是「機器學習」出場的地方了! 針對問題去選擇模型還有參數來做模型訓練，現在解決問題的答案不再只有傳統的經驗法則了，更有人工智慧、機器學習、深度學習、強化學習等等的方法。
4. 模型評估 (Model Evaluation)
   過程中我們可能會訓練出很多的模型並產生結果，這時候我們就要透過模型的驗證指標(Validation Index) 比較模型之間的好壞以及結果是否達到預期的狀態。如果未達預期的標準，可能就要去分析錯誤、不良的原因，重回上面幾個步驟進行改善，直到達到目的。

探索式資料分析 (Exploratory Data Analysis, EDA)

拿到新的資料時，我們一定要去做探索式資料分析，並看看資料的型態或是資料集中有沒有不尋常的數值出現。做探索式資料分析時，通常會從「敘述統計」或是「視覺化資料」先下手。

敘述統計 Descriptive Statistics

敘述統計就是直接去陳述資料或變數的統計量，以下是我在做敘述統計時常用的R指令:

看資料的整體:

數值統計:

補充:

• 計算平均時，若有遺失值，可以使用mean(na.omit())忽略遺失值進行計算。

• 計算相關係數時，根據變數的特性，可以選擇不同方式進行相關係數的計算，預設為cor(x1, x2, method = pearson)，其他方法包含 method = pearson, kendall, spearman。

skimr package

這邊再介紹一個很方便的packageskimr，package裡的skim( )函式會一次整理出資料集的統計資訊:

install.packages("skimr")
library(skimr)
skim(data) # data代入你的資料

以Iris data為例:

library(skimr)
skim(iris) 

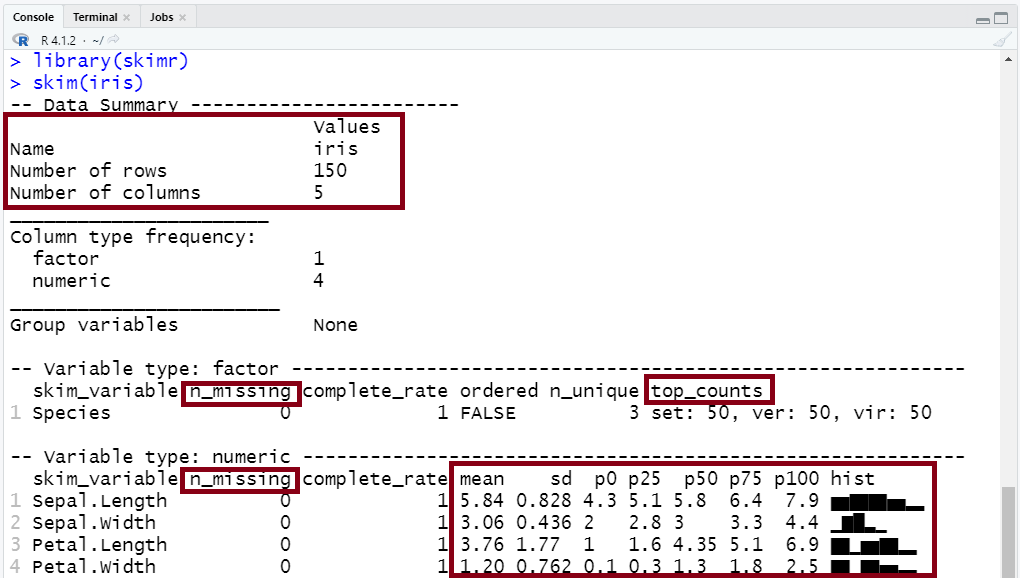
從 Console 的結果由上而下依序來看，我們可能會去注意看資料的:

• 資料名稱、資料比數、變數數目
• 各欄位(變數)的型態
• 遺失值數目
• 類別變數(有幾種不同種類、數量前幾多的類別各有多少筆資料)
• 數值變數(平均、標準差、最小值、四分位數、最大值、直方圖)

資料視覺化 Data Visualization

在資料視覺化的過程中，我們可能就已經能從資料中得到許多的資訊，包括:

• 是否有離群值
• 集中、離散(分散)程度
• 整體的趨勢
• 變數之間的相關性...

資料視覺化的相關筆記預計在別天做更詳細的補充，以下先提供幾種內建基礎的資料視覺化程式碼。

以Iris data為示範:

data(iris)
summary(iris)# 連續型資料:會看到 Qu.    #類別型資料:會看到不同類別的資料個數 
head(iris)   # 觀看前6筆資料
str(iris)    # 列出資料內每個欄位的狀態
class(iris$Species)
table(iris$Species) # 不同種類各有多少筆資料

hist(iris$Sepal.Length)
barplot(table(iris$Species))
pie(table(iris$Species))
plot(iris$Sepal.Length,iris$Petal.Length)
boxplot(iris$Sepal.Length)
stem(iris$Sepal.Length)

##補充
#另一種方便的barplot繪圖方式
library(lattice)
barchart(iris$Species)

補充:
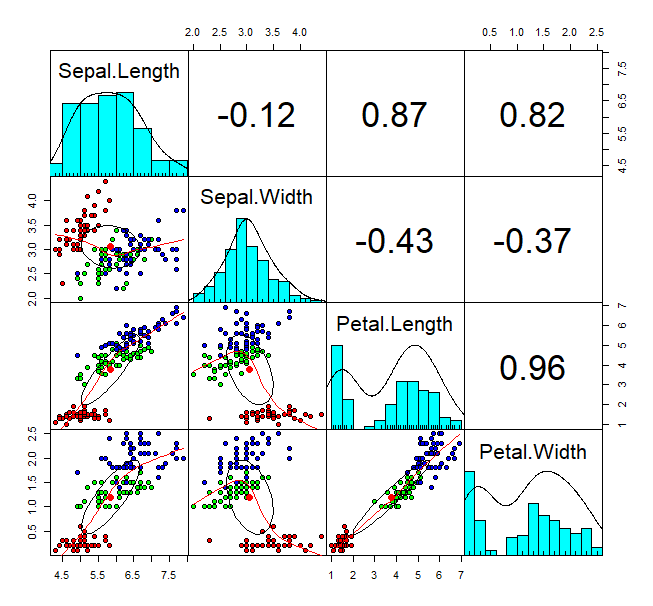
畫畫看散布圖矩陣(SPLOM):

# 進階: 畫出前四項變數的scatter diagram, histogram, & correlation values
install.packages("psych")
library(psych)
data(iris)
pairs.panels(iris[1:4],
             gap = 0,   #圖與圖之間的空隙
             bg = c("red", "green", "blue")[iris$Species],#將樣本根據Species分別套色
             pch = 21)  #pch 點的圖形

參考網站

Describing Datasets
https://medium.com/@amanann/describing-datasets-76b221d7d517

探索式資料分析如何做？ (@Tony Lee)
https://www.sightingdata.com/post/how-to-do-eda/